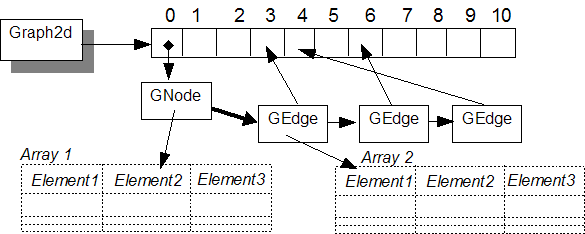
Representation of a graph with 11 nodes. The node #1 represents the element #2 of the array #1. The edge #0 has the neighbour nodes 3, 4 and 6. The edge #1 is described by the element #1 of the array #2.
The two types of graph are supported: directed and undirected graphs. With undirected graph, edges are symmetrical and with directed graph edges are non symmetrical.
The graph is disconnected from the array of objects it organizes. An index in each node is the mean to reference an object in a separate array, as a pointer, but without using a specified type. This principle allows the definition of any type of graph (with the same graph type): a graph of points, a graph of region maps, a graph of images, etc. This implies to define at the same time the graph and the array of objects. For example, to define a graph of region maps, one has to define a graph and an array of region maps. In the same way, edges can be described by an external array which lists properties for each edges.
GNode) is characterized by:
Each node i is characterized by an integer --accessible by g[i]->Item()-- which indexes an element in the array of elements. For example, suppose the structure of elements tab that contains at least the field size and a graph grs:
struct element tab[50]; // An array of 50 elements (Long). id=grs[i]->Item(); // id is the index in the array of objects. tab[id].size=120; // Sets the size of the object to 120 pixels.
GEdge) is characterized by its weight which is a Double value and an index to an external array that can describe the properties of the edge. Several edges can be created between two nodes. Each edge is identified by an index with can be used to reference an external array that decribes the edge properties.

Representation of a graph with 11 nodes. The node #1 represents the element #2 of the array #1. The edge #0 has the neighbour nodes 3, 4 and 6. The edge #1 is described by the element #1 of the array #2.
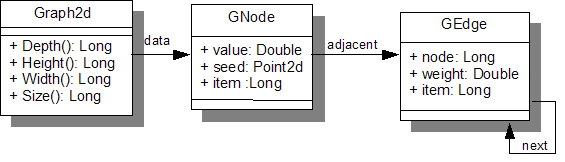
The class diagram for Graph2d.
Graph2d: graph in 2DGraph3d: graph in 3D.bool isDirected(): returns true if the graph is directed, false otherwise.Long Size(): returns the number of nodes;Long Width(): returns the number of columns of the related space;Long Height(): returns the number of rows of the related space;Long Depth(): returns the number of planes of the related space;Dimension ImageSize(): returns the dimension of the related space;PobjectProps Props(): returns a structure with the graph attribute values.Double value: stores the value of the node;Long Item([int x]): returns (if x is omitted) or sets (if x is given) the index of the element in the array of elements;Point2d seed: stores the coordinates of the node;GEdge* Neighbours(): returns the list of neighbour nodes.Long Node(): returns the node number of the neighbour;Long Item([int x]): returns (if x is omitted) or sets (if x is given) the index of the element in the array of elements;Double weight: stores the weight;GEdge* Next([GEdge* x]): returns (if x is omitted) or sets (if x is given) the next neighbour.Graph2d( bool directed =false); Graph2d( Long s, bool directed =false ); Graph2d( Long s, Long h, Long w, bool directed =false ); Graph2d( Long s, const Dimension2d &d, bool directed =false); Graph2d( const PobjectProps &p ); Graph3d( bool directed =false); Graph3d( Long s, bool directed =false ); Graph3d( Long s, Long d, Long h, Long w, bool directed =false ); Graph3d( Long s, const Dimension3d &d, bool directed =false); Graph3d( const PobjectProps &p );
For example, to create a new directed graph with or without related data, use:
Graph2d g(100,256,512,false); // Data: 100 nodes; Space: 256 rows x 512 columns. Graph2d g; // No data, no space. Graph2d *g=new Graph2d(200); // Data: 200 nodes; no space. Graph3d g(10,10,25,12,false); // Data: 10 nodes; Space 10 planesx25 rowsx12 columns Graph3d g; // No data; No Space, and undirected.
For example to create a new directed graph with or without related data, use:
Graph2d g(100,256,512,true); // Data: 100 nodes; Space: 256 rows x 512 columns. Graph2d g(true0; // No data, no space. Graph2d *g=new Graph2d(200,true); // Data: 200 nodes; no space. Graph3d g(10,10,25,12,true); // Data: 10 nodes; Space 10 planesx25 rowsx12 columns Graph3d g(true); // No data; No Space, and undirected.
To create a graph from the properties of another Pandore object, use:
Graph2d s1(obj2.Props());
obj2 is a graph then the number of nodes of gs1 is equal to the number of node obj2. If obj2 is a region map then the number of nodes of graph gs1 is equal to the higher value of labels +1. If obj2 is an image then the number of nodes of graph gs1 is equal to the number of pixels.New() allocates the data. If the data already exist they are deleted before the reallocation. For example: g.New(100,256,128); Graph2d *gs1; gs1->New(100,256,128);
To create a new graph from a region map use the member function Init(Reg2d &rgs). Seeds are set to the coordinates of the upper left point of the region (not the centre of mass). For example:
Reg2d rgs(100,100);
Graph2d grs(false);
grs.Init(rgs);
To create a new graph from a region map rgs and a seed map seed -seeds are given as punctual regions in a region map- use the member function Init(const Reg2d &rgs, const Reg2d &seed). For example:
Reg2d rgs1; Reg2d seed; grs.Init(rgs1,seed);
To create a graph from an another graph use operator =. For example:
Graph2d gs1(grs2->Props()); gs1 = grs2;
Delete(). For example: Graph2 gs1(12,256,256); gs1.Delete(); gs1.New(120,256,256); gs2->Delete();
Add(). For example, to add the node 5 that indexes the element 6 at the 3D coordinates z=50, y=12, x=10: grs.Add(5,6,Point3d(50,12,10));
The shorter instruction
grs.Add(5,6);
To get the index of the element represented by node s1 use the member function Item(). For example:
Long nbreg = g[i]->Item();
g[i] does not always exit, for instance when a node has been deleted with the member function Del(). So it is necessary to check first the existence of the node before using it: if ((g[i]!=NULL))
... g[i]-> ...
s from the graph, use the member function Del(). For example: grs.Del(10); // delete node 10.
s1 in the list of neighbours of the node s2 use the member function link(). An edge is created between s1 and s2, and if the graph is undirected the symmetrical edge between s2 and s1 is also added. If the edge already exists the weight is updated either by setting a new value if parameter add=false or by adding the new value to the current value if add=true. By default, the weight value is 1.0.For example, to create an edge between nodes 10 and 12 with weight=1.0:
grs.Link(10,12);
For example, to add the value 5.0 to the current value of the weight:
grs.Link(10,12,5.0,true);
To create several edges between two nodes; it is necessary to identify each edge with an integer. This integer can next be used to reference an external array that described the edge properties. For example, the following code snippet defines an array with a color for each edge. The edge between the node 10 and 12 is created and indexed with the 20th and the 22th colors.
Color[100] colors; grs.Link(10,12,20); grs.Link(10,12,22);
To get the list of neighbours of a node use the member function Neighbours(). For example:
GEdge* l = g[i]->Neighbours();
l=l->Next();
for (GEdge* l = g[i]->Neighbours(); l!=NULL; l=l->Next())
Long node = ptr->Node();
s1 from the list of neighbours of node s2 use the member function Unlink(Long s1,Long s2). If the graph is undirected the symmetrical edge is also deleted. For example: grs.Unlink(10,12);
If several edge are used between nodes, use the edge index to delete a specified edge. For example, to delete the edge indexed by 2:
grs.Unlink(10,12,2);
Graph2d grs;
grs.SaveFile("foobar.pan");
To load a graph from a file, just use:
Graph2d grs;
grs.LoadFile("foobar.pan");
Merge() merges 2 nodes (n1 and n2) into 1 node. Is also merges the list of neighbours. The node n1 is kept and the node n2 is deleted. The list of edges of node n2 is added to the list of edges of node n1. The weight of the common edges are added. For example: Graph2d grs;
Reg2d rgs(120,102);
grs.Init(rgs);
Reg2d::ValueType r1=10,r2=12;
gd.Merge(r1,r2); // Merges regions r1 and r2.
Split() splits one node into two nodes. The new node is a copy of the old node. Both nodes have the same attribute values and the same list of neighbours. For example: Graph2d grs;
Reg2d rgs(120,102);
grs.Init(rgs);
Reg2d::ValueType r1=10,r2=120;
gd.Split(r1,r2); // Split region r1 in r1 and r2.