Tutoriel : Correction de l'illumination

La correction prospective utilise des images additionnelles obtenues au moment de l'acquisition de l'image à traiter. Deux types d'images additionnelles peuvent être acquises :

• Une image noire est une image du fond de la scène acquise sans lumière.
• Une image blanche est une image du fond de la scène acquise avec lumière mais sans objet.

dark = ∑ darki
bright = ∑ brighti

1. Correction à l'aide des images noire et blanche

L'image corrigée g(x,y) est obtenue en utilisant la transformation suivante :

            f(x,y) - d(x,y)
   g(x,y) = --------------- .C
            b(x,y) - d(x,y)

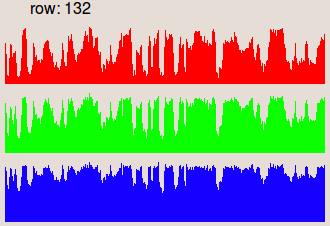
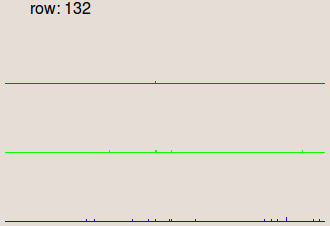
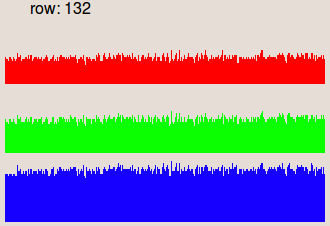
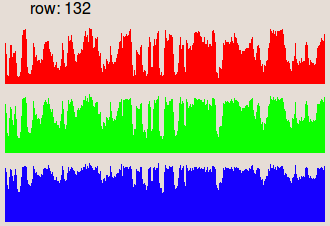
où f(x,y) est l'image originale, d(x,y) est l'image noire, b(x,y) est l'image blanche, et C est la constante de normalisation qui permet de recouvrer les couleurs de l'image originale :

                                  1
    C = mean(f(x,y)) . ----------------------
                           f(x,y) - d(x,y) 
                     mean( --------------- )
                           b(x,y) - d(x,y)  

avec mean(i(x,y)) la valeur moyenne de l'image i(x,y).

Script Pandore (bash)

psub serous.pan dark.pan tmp1.pan
psub bright.pan dark.pan tmp2.pan
pdiv tmp1.pan tmp2.pan tmp3.pan
pmeanvalue tmp3.pan c1.pan
pdivval c1.pan tmp3.pan tmp4.pan
pmeanvalue serous.pan c2.pan
pmultval c2.pan tmp4.pan output.pan

Résultat

Les images sur la seconde ligne représentent les profils de la ligne 132, où les niveaux de gris sont présentés sous la forme de barres verticales. On peut constater sur l'image originale que l'éclairage est plus faible à gauche qu'à droite. Ce défaut a été corrigé sur l'image résultat.

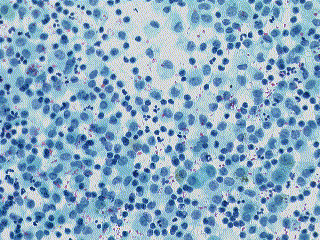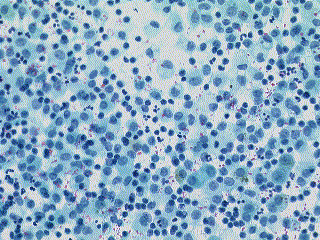
Image originale.	Image noire.	Image blanche.	image résultat corrigée.
Profil de la ligne 132.	Profil de la ligne 132.	Profil de la ligne 132.	Profil de la ligne 132.

2. Correction à l'aide de l'image blanche seule

Si seule l'image blanche existe, la méthode utilise une division de l'image source avec l'image blanche si le capteur est linéaire, ou une soustraction de l'image source avec l'image blanche si le capteur est logarithmique avec un gamma de 1.

Dans le cas d'un capteur d'acquisition linéaire, l'image corrigé g(x,y) est obtenue en utilisant la transformation suivante :

            f(x,y)
   g(x,y) = ------ . C
            b(x,y)

où f(x,y) est l'image originale, b(x,y) est l'image blanche, et C la constante de normalisation qui permet de recouvrer les couleurs de l'image originale :

                           1
   C = mean(f(x,y)) . ------------
                           f(x,y)
                     mean( ------ )
                           b(x,y)

où mean(i(x,y)) est la valeur moyenne de l'image i(x,y).

Script Pandore (bash)

pdiv grain.pan grain_background.pan tmp1.pan
pmeanvalue grain.pan c1.col
pmultval c1.col tmp1.pan tmp2.pan
pmeanvalue tmp1.pan c2.col
pdivval c2.col tmp2.pan grain_out.pan

Résultats

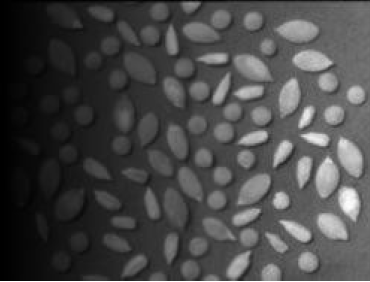
L'effet d'éclairage est plus prononcé à gauche qu'à droite.

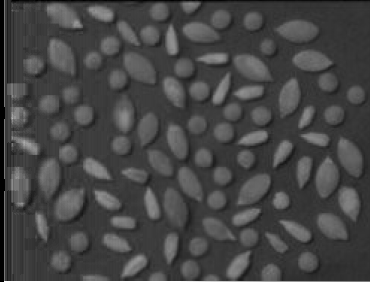Image originale.	Background image.	Image résultat.
Profil de la ligne 132.	Profil de la ligne 132.	Profil de la ligne 132.

3. Correction à l'aide de l'image noire seule

Si seule l'image noire existe, la méthode consiste à soustraire l'image noire de l'image originale. Le but est de corriger un défaut lié au capteur. L'image corrigée g(x,y) est alors obtenue en utilisant la transformation suivante :

   g(x,y) = f(x,y) - d(x,y) + mean(d(x,y))

où f(x,y) est l'image originale, d(x,y) est l'image noire et mean(d(x,y)) est la valeur moyenne de l'image noire.

Script Pandore (bash)

psub serous.pan dark.pan tmp1.pan
pmeanvalue dark.pan c.col
paddval c.col tmp1.pan out.pan

Résultats

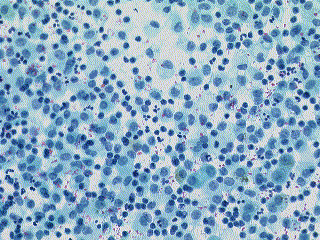Image originale.	Dark image.	Image résultat.
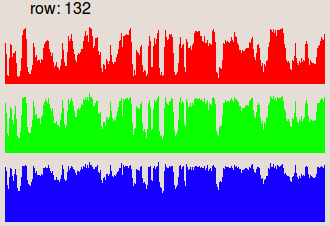Profil de la ligne 132.	Profil de la ligne 132.	Profil de la ligne 132.

II. Correction rétrospective

Quand les images additionnelles ne sont pas disponibles, un modèle idéal de l'illumination doit être estimé pour construire l'image blanche. La correction rétrospective utilise alors la même technique de suppression du fond que la correction prospective en utilisant cette image blanche estimée.

Il y a différentes techniques pour estimer l'image blanche. Toutes supposent que les objets correspondent aux hautes fréquences et le fond de la scène aux basses fréquences. La correction rétrospective consiste à supprimer les objets du fond pour construire l'image blanche puis à appliquer la même technique que la correction prospective.

1. Correction rétrospective à base de filtre passe-bas

Le fond d'image est estimé par un filtre passe-bas de grande taille. Le fond estimé est ensuite soustrait de l'image initiale pour compenser le défaut d'illumination.
L'image corrigée g(x,y) est obtenue à partir de l'image initiale f(x,y) par :

   g(x,y) = (f(x,y) - LPF(f(x,y))) + mean(LPF(f(x,y)))

où LPF(f(x,y)) est l'image filtrée et mean(LPF(f(x,y))) est la moyenne des valeurs des pixels de l'image filtrée.

L'exemple utilise un filtre gaussien de taille 20, supérieure à la taille des objets (ici les caractères).

Script Pandore (bash)

pgaussianfiltering 20 page.pan mask.pan
psub page.pan mask.pan tmp.pan
pmeanvalue mask.pan c.col
paddval c.col tmp.pan out.pan

Résultats

Image originale.	Image du fond estimé.	Image résultat.
Profil de la ligne 132.	Profil de la ligne 132.	Profil de la ligne 132.

2. Correction rétrospective à base de filtre homomorphique

Le fond d'image est estimé par un filtre homomorphique passe-bas. Le principe du filtrage homomorphique est de supprimer les hautes-fréquences (considérées comme la réflectance) et de garder les basses-fréquences (considérées comme l'illumination). Le fond est supprimé par un filtrage passe-haut du logarithme de l'image puis en prenant l'exponentiel pour restaurer l'image.

L'image corrigée g(x,y) est obtenue à partir d'image initiale f(x,y) par :

   g(x,y) = exp(LPF(log(f(x,y)))) . C

où LPF(i(x,y)) est l'image i(x,y) filtrée par un filtre passe-bas et C est le coefficient de normalisation donné par :

              mean(f(x,y))
   C = ----------------------------
                  f(x,y)
       mean( --------------------- )
              exp(LPF(log(f(x,y))))

où mean(i(x,y)) est la valeur moyenne de l'image i(x,y).

L'exemple suivant utilise le filtre de Butterworth avec une valeur de coupure de 3.

Il faut noter que cette technique n'est pas très efficace pour corriger les défauts d'illumination.

Script Pandore (bash)

cutin=0
# the less the cutoff value, the stronger filtering.
cutoff=3
order=2

homomorphicfiltering(){
    paddcst 1 $1 i0.pan # The zero log problem
    plog i0.pan i0.pan
    psetcst 0 i0.pan i1.pan
    pfft i0.pan i1.pan i2.pan i3.pan
    pproperty 0 i2.pan
    ncol2=`pstatus`
    pproperty 1 i2.pan
    nrow2=`pstatus`
    pproperty 2 i2.pan
    ndep2=`pstatus`
    pbutterworthfilter $ncol2 $nrow2 $ndep2 0 $cutin $cutoff $order i4.pan 
    pmult i2.pan i4.pan i5.pan
    pmult i3.pan i4.pan i6.pan
    pifft i5.pan i6.pan i7.pan i8.pan
    
    pproperty 0 $1
    ncol1=`pstatus`
    pproperty 1 $1
    nrow1=`pstatus`
    pproperty 2 $1
    ndep1=`pstatus`

    pextractsubimage 0 0 0 $ncol1 $nrow1 $ndep1 i7.pan i9.pan
    pexp i9.pan i11.pan
    paddcst -1 i11.pan i12.pan
    
    pclipvalues 0 255 i12.pan  i13.pan
    pim2uc i13.pan $2
}
    
multiplicative-correction() {
    pdiv $1 $2 i14.pan
    pmeanvalue $1 col.pan; c1=`pstatus`
    pmeanvalue i14.pan col.pan; c2=`pstatus`
    c=`echo "scale = 1; $c1/$c2" | bc`
    
    pmultcst $c i14.pan $3
}

pproperty 3 page.pan; bands=`pstatus`
if [ $bands -eq 1 ]
then
    # grayscale image
    homomorphicfiltering page.pan mask2.pan
    multiplicative-correction page.pan mask2.pan out.pan
else
    # color image
    pimc2img 0 input1.pan r.pan
    pimc2img 1 input1.pan g.pan
    pimc2img 2 input1.pan b.pan
    homomorphicfiltering r.pan maskr.pan
    homomorphicfiltering g.pan maskg.pan
    homomorphicfiltering b.pan maskb.pan
    multiplicative-correction r.pan maskr.pan outr.pan
    multiplicative-correction g.pan maskg.pan outg.pan
    multiplicative-correction b.pan maskb.pan outb.pan 
    pimg2imc 0 outr.pan outg.pan outb.pan out.pan
fi

Résultats

Image originale.	Image du fond estimé.	Image résultat.
Profil de la ligne 132.	Profil de la ligne 132.	Profil de la ligne 132.

3. Correction rétrospective à base de filtre morphologique

Le fond d'image est estimé par application de filtres de fermeture ou d'ouverture issues de la morphologie mathématique. Le fond estimé est ensuite soustrait de l'image initiale. La séquence d'opérations correspond à l'application d'un chapeau haut-de-forme sur l'image. Le chapeau haut-de-forme supprime les hautes fréquences (considérées comme la réflectance) et garde les faibles fréquences (considérées comme l'illumination). Le chapeau haut-de-forme noir est adapté à un fond clair et le chapeau haut-de-forme blanc est adapté à un fond sombre.

Si le fond est plus clair qur les objets, l'image corrigée g(x,y) est obtenue par :

   g(x,y) = BTH[f(x,y)] + mean(closing(f(x,y)))
   g(x,y) = [f(x,y) - closing(f(x,y))] + mean(closing(f(x,y)))

où mean(closing(f(x,y))) est la moyenne des niveaux de gris de l'image résultant de la fermeture.

L'exemple suivant utilise un élément structurant de type disque de taille 11 supérieure à la taille des objets (ici les caractères).

Script Pandore (bash)

# black top hat
pdilatation 2 5 page.pan b.pan
perosion 2 5 b.pan mask3.pan
psub page.pan mask3.pan tmp.pan
# normalization
pmeanvalue mask3.pan c.col
paddval c.col tmp.pan out.pan

Résultats

Image originale.	Image du fond estimé.	Image résultat.
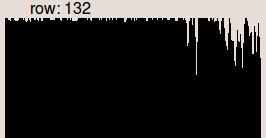Profil de la ligne 132.	Profil de la ligne 132.	Profil de la ligne 132.

4. Correction rétrospective à base de régression linéaire

Cette technique permet d'approximer le fond de la scène par un plan en utilisant une régression linéaire orthogonale. Le fond est approximé par un plan, donc la technique n'est pas très adaptée à un fond complexe.

L'image corrigée g(x,y) est obtenue à partir de l'image initiale f(x,y) par :

   g(x,y) = (f(x,y) - LR(f(x,y)) - mean(LR(f(x,y)))

où LR(f(x,y)) est l'image obtenue par régression linéaire en x et y de f(x,y), et mean(LR(f(x,y))) est la valeur moyenne de cette image.

Script Pandore (bash)

plinearregression page.pan mask4.pan
psub page.pan mask4.pan tmp.pan
pmeanvalue mask4.pan c.col
paddval c.col tmp.pan out.pan

Résultats

Image originale.	Image du fond estimé.	Image résultat.
Profil de la ligne 132.	Profil de la ligne 132.	Profil de la ligne 132.

5. Correction rétrospective par approximation polynomiale de la surface

Le fond d'image est approximé par un polynôme obtenu à l'aide des moindres carrés. Le fond est ensuite soustrait de l'image initiale pour compenser l'illumination. L'image corrigée g(x,y) est obtenue à partir de l'image initiale f(x,y) par :

   g(x,y) = (f(x,y) - b(f(x,y))) - mean(b(f(x,y)))

où b(f(x,y)) est l'image obtenue à partir de l'approximation polygonale du fond d'image, et mean(b(f(x,y))) est la valeur moyenne de l'image du polynôme.

L'approximation polygonale consiste à approximer une fonction à partir d'un nombre de points ((x,y), f(x,y)) par un polynôme d'un degré choisi et qui passe par tous les points. Dans les exemples suivants, deux types de polynômes ont été utilisés :

• polynôme du second ordre
• polynôme de Legendre.

Polynôme du second ordre

Le premier exemple suivant utilise un polynôme de second ordre. L'opérateur nécessite un masque pour sélectionner les pixels qui appartiennent au fond. Le masque définit la liste des pixels du fond qui sont utilisés pour calculer les valeurs du polynôme.

L'ordre des termes du polynôme peut être sélectionné différemment pour x, y et les termes mixtes. Par exemple, avec l'ordre 2, 3 pour x, y, et l'ordre 2 pour xy, le polynôme devient :

  a+b*x+c*x^2+d*y+e*y^2+f*y^3+g*xy

Script Pandore (bash)

ppolynomialfitting 2 2 1 page.pan page_mask.pan mask5.pan
psub page.pan mask5.pan tmp.pan
pmeanvalue mask5.pan c.col
paddval c.col tmp.pan out.pan

Résultats

Image originale.	Image masque.	Image du fond estimé.	Image résultat.
	.
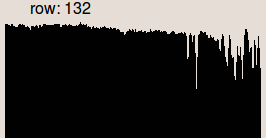Profil de la ligne 132.	.	Profil de la ligne 132.	Profil de la ligne 132.

Polynôme de Legendre

Le second exemple utilise un polynôme de Legendre. Cette technique utilise la relation d'orthogonalité des polynômes de Legendre pour étendre une image comme une double somme de ces fonctions. La somme est ensuite évaluée pour produire une image qui approxime une projection dans l'espace de l'image de polynôme.

Script Pandore (bash)

plegendrepolynomialfitting 2 2 page.pan mask6.pan
psub page.pan mask6.pan tmp.pan
pmeanvalue mask6.pan c.col
paddval c.col tmp.pan out.pan

Résultats

Image originale.	Image du fond estimé.	Image résultat.
Profil de la ligne 132.	Profil de la ligne 132.	Profil de la ligne 132.

6. Correction rétrospective pour les images couleur

Les méthodes présentées précédemment ne s'appliquent pas telles que aux images couleur parce qu'elles utilisent des opérations bandes par bandes et donc altèrent les couleurs (création de nouvelles couleurs).

La solution est de convertir l'image dans l'espace couleur HSL puis d'appliquer les corrections précédentes sur la bande correspondant à la luminosité.