 Équipe IMAGE - Le projet Pantheon
Équipe IMAGE - Le projet Pantheon
Le redimensionnement ou le ré-échantillonnage est une technique qui permet de créer une nouvelle version d'une image avec une taille différente. L'augmentation de la taille est appelée sur-échantillonnage, et la réduction de la taille de l'image est appelée sous-échantillonnage.
Il s'avère que ces opérations ne sont pas sans perte. Par exemple, si on sous-échantillonne une image puis sur-échantillonne, on obtient un résultat légèrement différent de l'image initiale.
De plus, le redimensionnement n'est pas un processus trivial. Il implique nécessairement un compromis entre efficacité, lissage et netteté. C'est pourquoi il existe différents algorithmes. Pandore contient plusieurs algorithmes pour faire du redimensionnement. Chacun a ses avantages et inconvénients en termes de pertes, flou et vitesse.
Nous présentons ici une liste d'exemples qui utilisent des opérateurs Pandore pour réaliser la transformation. Nous discutons du cas du sur-échantillonnage et du sous-échantillonnage séparément parce que les algorithmes peuvent avoir des comportements différents dans chaque cas.
Le sur-échantillonnage est illustré sur l'imagette ci-dessous qui est agrandie de 400% (x 4).

 |
 |
| Ré-échantillonnage au plus proche voisin | Ré-échantillonnage bilinéaire |
|---|---|
prescale 4 4 0 jellybeans.pan result.pan |
plinearrescale 4 4 0 jellybeans.pan result.pan |
 |
 |
| Ré-échantillonnage de Hermite | Ré-échantillonnage de Bell |
phermiterescale 4 4 0 jellybeans.pan result.pan |
pbellrescale 4 4 0 jellybeans.pan result.pan |
 |
 |
| Ré-échantillonnage de Mitchell | Ré-échantillonnage bicubique |
pmitchellrescale 4 4 0 jellybeans.pan result.pan |
pbicubicrescale 4 4 0 jellybeans.pan result.pan |
 |
|
| Ré-échantillonnage de Lanczos | |
planczosrescale 4 4 0 jellybeans.pan result.pan |
Le sur-échantillonnage est illustré sur l'imagette ci-dessous qui est agrandie de 400% (x 4).

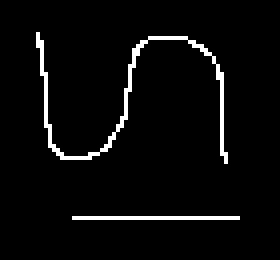 |
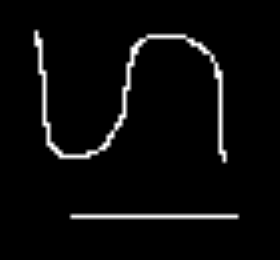 |
| Ré-échantillonnage au plus proche voisin | Ré-échantillonnage bilinéaire |
|---|---|
prescale 4 4 0 binarysmall.pan result.pan |
plinearrescale 4 4 0 binarysmall.pan result.pan |
 |
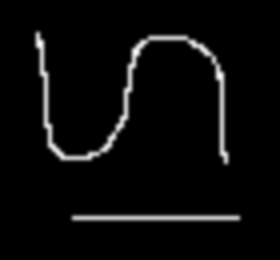 |
| Ré-échantillonnage de Hermite | Ré-échantillonnage de Bell |
phermiterescale 4 4 0 binarysmall.pan result.pan |
pbellrescale 4 4 0 binarysmall.pan result.pan |
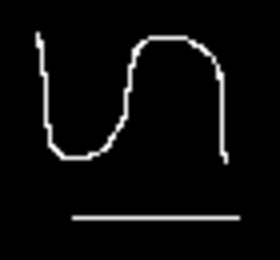 |
 |
| Ré-échantillonnage de Mitchell | Ré-échantillonnage bicubique |
pmitchellrescale 4 4 0 binarysmall.pan result.pan |
pbicubicrescale 4 4 0 binarysmall.pan result.pan |
 |
|
| Ré-échantillonnage de Lanczos | |
planczosrescale 4 4 0 binarysmall.pan result.pan |
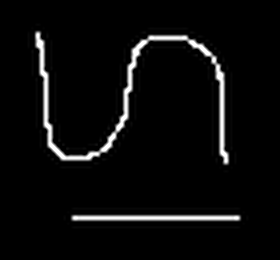
Le sous-échantillonnage est illustré sur l'image ci-dessous avec une réduction de 400% (x 0.4).

 |
 |
| Ré-échantillonnage au plus proche voisin | Ré-échantillonnage bilinéaire |
|---|---|
prescale 0.4 0.4 0 whiteboard.pan result.pan |
plinearrescale 0.4 0.4 0 whiteboard.pan result.pan |
 |
 |
| Ré-échantillonnage de Hermite | Ré-échantillonnage de Bell |
phermiterescale 0.4 0.4 0 whiteboard.pan result.pan |
pbellrescale 0.4 0.4 0 whiteboard.pan result.pan |
 |
 |
| Ré-échantillonnage de Mitchell | Ré-échantillonnage bicubique |
pmitchellrescale 0.4 0.4 0 whiteboard.pan result.pan |
pbicubicrescale 0.4 0.4 0 whiteboard.pan result.pan |
 |
|
| Ré-échantillonnage de Lanczos | |
planczosrescale 0.4 0.4 0 whiteboard.pan result.pan |
Le sous-échantillonnage est illustré sur l'image ci-dessous avec une réduction de 400% (x 0.4).

 |
 |
| Ré-échantillonnage au plus proche voisin | Ré-échantillonnage bilinéaire |
|---|---|
prescale 0.4 0.4 0 binary.pan result.pan |
plinearrescale 0.4 0.4 0 binary.pan result.pan |
 |
 |
| Ré-échantillonnage de Hermite | Ré-échantillonnage de Bell |
phermiterescale 0.4 0.4 0 binary.pan result.pan |
pbellrescale 0.4 0.4 0 binary.pan result.pan |
 |
 |
| Ré-échantillonnage de Mitchell | Ré-échantillonnage bicubique |
pmitchellrescale 0.4 0.4 0 binary.pan result.pan |
pbicubicrescale 0.4 0.4 0 binary.pan result.pan |
 |
|
| Ré-échantillonnage de Lanczos | |
planczosrescale 0.4 0.4 0 binary.pan result.pan |
Quand on agrandit une image, la question se pose de savoir quelle couleur mettre pour les nouveaux pixels qui apparaissent entre les pixels d'origine. Quand on rétrécit une image, la question inverse est de savoir quelle sera la couleur des pixels restants. Il existe plusieurs réponses à ces deux questions.
Pour simplifier la présentation, prenons le cas d'une image en 1D nommée f(x) que nous souhaitons agrandir d'un facteur de 2 pour donner une nouvelle image g(x). Mathématiquement, cela se formule par :
g(x) = f(x/2)
Prenons un exemple concret pour f(x) avec les valeurs [2, 3, 5, 4, 3, 2, 4]. Cela nous donne l'image ci-dessous (avec une représentation en coupe de l'image dans laquelle les niveaux de gris sont représentés en hauteur) :
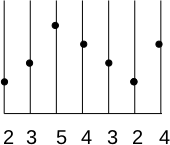
Ce que nous cherchons à faire, c'est doubler la taille de l'image f(x) pour obtenir g(x).
Donc, nous devons déterminer ce qui se passe entre les pixels connus.
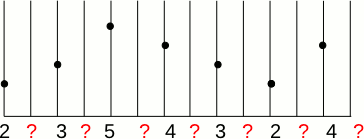
Il y a deux réponses immédiates :
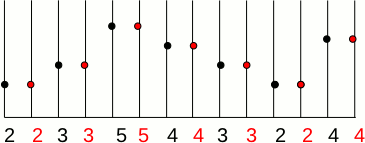
Si nous avions choisi de tripler la taille de l'image f(x), alors nous aurions obtenu l'image g(x) ci-dessous :
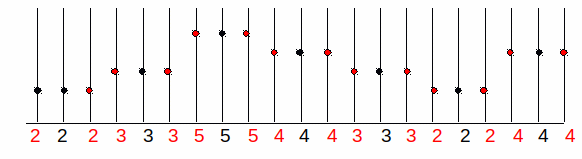
Pour réduire l'image de n fois en utilisant le principe inverse de la réplication au plus proche voisin, il suffit de prendre 1 pixel sur n.
La seconde solution consiste à prendre pour chaque pixel inconnu la moyenne pondérée par l'inverse de la distance au pixel inconnu des valeurs des pixels connus. Plus un pixel connu est loin, moins il contribue à la valeur de la couleur du pixel inconnu. Cela revient à tracer une ligne entre les deux pixels connus et prendre la valeur entière la plus proche de la ligne pour chaque pixel inconnu. Cette solution s'appelle « l'interpolation linéaire » puisque nous utilisons des lignes droites entre les échantillons.
En reprenant l'exemple du doublement de la taille de l'image, on obtient l'image g(x) ci-dessous qui n'utilise en fait qu'une moyenne classique puisque les deux pixels inconnus sont à la même distance. Par exemple, la valeur du premier pixel inconnu s'obtient par |(2+3)/2|=2, et le second |(3+5)/2|=4.

Pour réduire l'image par n, il suffit de prendre la moyenne des pixels de n en n.
On peut se demander laquelle des deux méthodes décrites jusqu'ici est la « meilleure ». La réponse est « ça dépend ». Dans le cas d'une image, la seconde méthode est certainement la meilleure puisque la première produit un effet de crénelage alors que la seconde donne une image plus lisse. Par contre, dans le cas d'une carte de régions, la première est la seule solution possible puisque la seconde méthode crée des valeurs de labels qui n'existaient pas dans l'image initiale.
Avant de passer à la 2D, nous allons examiner une manière moins intuitive mais plus générale pour mettre en œuvre ces méthodes : la convolution. La convolution définit un principe général pour faire de l'interpolation. Le noyau d'interpolation k(i) définit la liste des voisins à prendre en compte et le poids qui leur est affecté pour calculer la valeur du pixel central. Mathématiquement, cela correspond à l'opération :
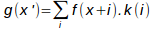
En choisissant les bons filtres, nous pouvons définir différents types de reconstruction. Par exemple, l'interpolation au plus proche voisin avec priorité à gauche pour doubler la taille est implémentée par le noyau de convolution [1, 1, 0]. L'interpolation linéaire peut être implémentée par le noyau [0.5 1 0.5]. Pour les autres distances, nous utilisons simplement d'autres noyaux. Par exemple, le noyau du plus proche voisin pour tripler la taille est [0, 1, 1, 1, 0] et le noyau d'interpolation linéaire est [1/3, 2/3, 1, 2/3, 1/3].
Pour illustrer le principe de l'interpolation avec un noyau de convolution, prenons le cas du noyau bilinéaire : on double la taille de f(x) et on met des 0 pour les nouveaux pixels (on obtient f'(x)). À partir de là, la convolution permet de construire g(x). Ainsi, la valeur à la coordonnée 6 est égale à 34 = 1*34+0*2/3+0*1/3+0*2/3+0*1/3.

Celle à la coordonnée 7 est égale à 39 = 1/3*50 + 2/3*34.

Cette mise en œuvre par convolution a plusieurs avantages :
Avec le principe de la convolution, il est facile de varier les types de noyaux et donc le type d'interpolation. Nous l'avons vu précédemment, le noyau le plus simple est celui de l'interpolation au plus proche voisin et correspond à une boîte. Cela produit en sortie une image qui présente des crénelages très prononcés du fait de la forme de la discrétisation.

L'interpolation linéaire utilise un noyau de convolution k(x) qui a la forme d'un triangle. L'image de sortie présente donc une surface plus douce puisque la discrétisation est moins prononcée.

Mais on peut encore adoucir la transition entre deux pixels en utilisant des courbes au lieu de droites.

En général on utilise les B-splines pour modéliser la transition entre deux pixels connus. Les B-splines sont des courbes décrites par une série de polynômes d'un degré donné. Plus le degré est élevé plus la courbe autorise de variation dans la courbe.
Une spline de degré 1 est formée par une suite de droites, et correspond donc à un noyau bilinéaire. Une spline de degré 2 est composée d'une série de courbes paraboliques et une B-spline de degré 3 est une série de courbes cubiques.
Tout ce que nous avons dit en 1D s'applique également en 2D et 3D. La seule différence est que la convolution s'effectue à la fois en x, y et z. Par exemple en 2D, la convolution s'écrit :
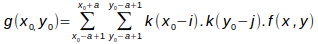
Dans ce qui suit, nous présentons les différents noyaux d'interpolation existants en 2D et 3D dans la bibliothèque Pandore.
La couleur d'un pixel dans l'image résultat est la couleur du plus proche pixel correspondant dans l'image originale. Si on agrandit l'image par 2, un pixel sera recopié 4 fois dans l'image originale, ce qui produit un carré de taille 4 pixels avec la même couleur. Si on réduit l'image par 2, seulement un pixel sur 2x2 est retenu dans l'image résultat.
Le noyau de convolution k(x) est donc simplement :
k(x) = | 1 ; si |x| < 0.5
| 0 ; sinon
|
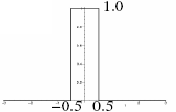
|
Cet opérateur produit un effet de blocs dans le cas d'un sur-échantillonnage et supprime les contours fins dans le cas d'un sous-redimensionnement. Cependant, il est rapide et c'est le seul qui n'ajoute pas de nouvelles couleurs dans l'image.
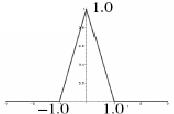
Le ré-échantillonnage bilinéaire considère les 2x2 voisins les plus proches du pixel inconnu pour calculer la valeur. Le noyau de convolution triangulaire k(x) est donc :
k(x) = | 1-|x| ; |x| < 1
| 0 ; sinon
|
|
Le ré-échantillonnage de Bell utilise un noyau de convolution pour interpoler les pixels de l'image initiale afin de calculer la valeur des pixels de l'image résultat. Le noyau de convolution de Bell k(x) est défini par:
| 0.75-|x|2 ; si |x| < 0.5
k(x) = | 0.5 * (|x|-1.5)2 ; si 0.5 < |x| <1.5
| 0 ; sinon
|
Le ré-échantillonnage de Hermite utilise un noyau de convolution pour interpoler les pixels de l'image initiale afin de calculer la valeur des pixels de l'image résultat. Hermite est un cas particulier de l'algorithme bicubique, où a=0. Le noyau de convolution de Hermite k(x) est défini par:
k(x) = | 2|x|3 - 3|x|2 + 1 ; si |x| ≤ 1
| 0 ; sinon
|
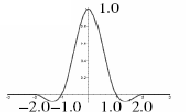
Pour le ré-échantillonnage bicubique, le noyau de convolution est composé par partie de polynômes cubiques. La valeur d'un pixel de sortie est calculée par la somme pondérée de ses 4x4 voisins. Le noyau de convolution k(x) est :
| (a+2)|x|3 - (a+3)|x|2+1 ; si |x| ≤ 1
k(x) = | a|x|3 - 5a|x|2 +8a|x| - 4a ; si 1 < |x| < 2
| 0 ; sinon
où a est égal à -0.5 dans la présente implémentation. A noter que si a=0, l'algorithme est équivalent à celui de Hermite. |
|
C'est probablement le plus utilisé des algorithmes de ré-échantillonnage dans les logiciels de retouche d'images puisqu'il présente un bon compromis entre efficacité et rapidité.
Le ré-échantillonnage de Mitchell utilise un noyau de convolution pour interpoler les pixels de l'image initiale afin de calculer la valeur des pixels de l'image résultat. C'est aussi un filtre bicubique.
Le noyau de convolution de Mitchell k(x) est défini par :
où B=1/3, et C=1/3
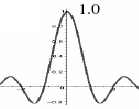
L'algorithme de Lanczos utilise un noyau de convolution pour interpoler les pixels de l'image initiale de façon à calculer les valeurs des pixels de l'image de sortie. Le noyau de convolution de Lanczos k(x) est défini par :
|
Cet algorithme fournit les meilleurs résultats, mais est très chronophage.